|
Algèbre de
Boole
Un interrupteur (C1 ou C2) peut prendre
deux états :
« fermé » (le courant passe) ou « ouvert
».
Considérons le circuit électrique suivant
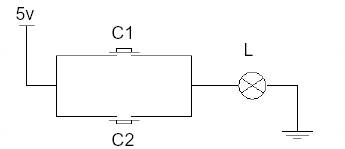
De même, la lampe peut prendre deux
états :« allumée » ou « éteinte ».
La lampe « L » est allumée si et seulement
si l ’un des interrupteurs C1 ou C2
est fermé
Par convention, posons :
- « fermé » = « allumé » = « 1
» (= « VRAI »)
- « ouvert » = « éteint » = « 0
» (=« FAUX »).
C1, C2 et L sont des variables
logiques et la fonction qui permet
de calculer L à partir de C1 et C2 est
une fonction logique, c ’est
la fonction « ou ».
On énumère les différentes configurations
possibles
|
C1
|
C2
|
L
|
|
Ouvert
|
ouvert
|
éteinte
|
|
ouvert
|
fermé
|
allumée
|
|
fermé
|
ouvert
|
allumée
|
|
fermé
|
fermé
|
allumée
|
On note la fonction « ou » par
le symbole « + », on a : L=C1+C2.
Le tableau de toutes les configurations
s ’appelle « la table de vérité »
et s ’écrit :
|
C1
|
C2
|
C1 + C2
|
|
0
|
0
|
0
|
|
0
|
1
|
1
|
|
1
|
0
|
1
|
|
1
|
1
|
1
|
Autre nom : « disjonction »
Fonction
« et »
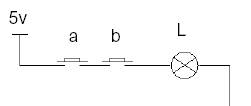
La lampe L est allumée si et seulement
si les interrupteurs a et b sont fermés.
Cette fonction est notée « . »,
c ’est la conjonction
|
a
|
b
|
a.b
|
|
0
|
0
|
0
|
|
0
|
1
|
0
|
|
1
|
0
|
0
|
|
1
|
1
|
1
|
Les fonctions à une
seule variable :
Fonction négation
(complémentation) « NON » « NOT
»)
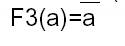
Principales Fonctions à deux variables
|
A
|
B
|
ET a.b
|
Ou exclusif
Xor
a Å b
|
Ou
a + b
|
nonOu
Nor
a ¯ b
|
Implication
b implique a
b ® a
|
Implication
a implique b
a ® b
|
nonEt
Nand
a b
|
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
|
0
|
1
|
0
|
1
|
1
|
0
|
0
|
1
|
1
|
|
1
|
0
|
0
|
1
|
1
|
0
|
1
|
0
|
1
|
|
1
|
1
|
1
|
0
|
1
|
0
|
1
|
1
|
0
|
Axiomes de base
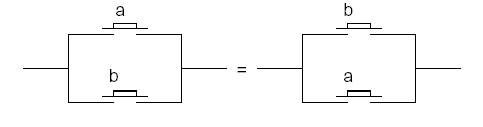
Commutativité :
a.b
= b.a
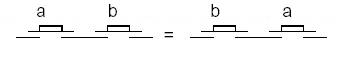
a
+ b = b + a
Associativité
a.(b.c) = (a.b).c
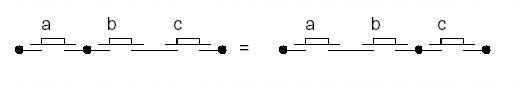
a + (b + c) = (a
+ b) + c
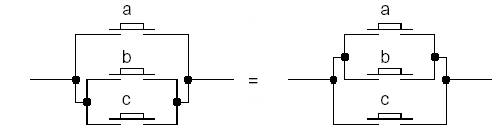
Distributivité :
a.(b + c) = (a.b)
+ (a.c)
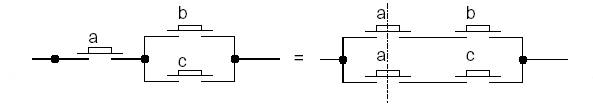
a + (b.c) = (a +
b).(a + c)
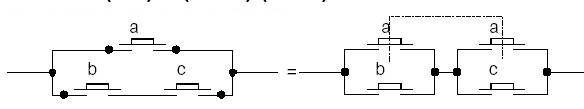
Eléments neutres
1.a = a.1 = a
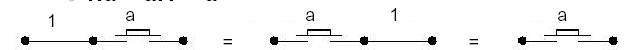
0
+ a = a + 0 = a

Complément

Elément absorbant :
a.0 = 0.a = 0
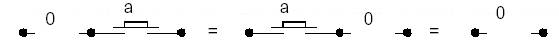
a + 1 = 1 + a = 1

Absorption :
a.(a
+ b) = a a + (a.b) = a
Idempotence :
a.a
= a
a + a = a
Involution :
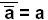
Théorème de De Morgan
:
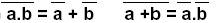
Notation binaire
Un nombre binaire est la représentation
d ’un nombre en base 2 (écrite exclusivement
avec des 0 et des 1).
Pour traduire un nombre binaire en décimal
(base10), on utilise la formule
:
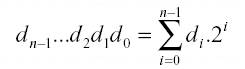
|